1010번: 다리 놓기
입력의 첫 줄에는 테스트 케이스의 개수 T가 주어진다. 그 다음 줄부터 각각의 테스트케이스에 대해 강의 서쪽과 동쪽에 있는 사이트의 개수 정수 N, M (0 < N ≤ M < 30)이 주어진다.
www.acmicpc.net
가끔 이런 문제들이 있습니다.
간단한 수학문제를, 아주아주 길고 긴 스토리 텔링을 통해 헷갈리게 해놓고
'히히 이거 사실 수학문젠데.... 알아 챌수 있닝???' 식의 문제죠..
이 문제는 조합으로 풀 수 있는 문제입니다.
하지만 역시 수가 매우매우 커질 것 같습니다.
조합으로 푸려다가 포기하셨다면, 제 코드가 도움이 될 것 같습니다.
[전체 코드 보기]
#include <iostream>
using namespace std;
int main()
{
int T, LeftSite, RightSite, temp, count = 0;
long long LeftFacto = 1, RightFacto = 1;
int LeftField[30] = { 0, }, RightField[30] = { 0, };
cin >> T;
for (int i = 0; i < T; i++)
{
cin >> LeftSite >> RightSite;//왼쪽 사이트와 오른쪽 사이트의 정보를 받는다.
temp = LeftSite;
for (int i = 0; i < temp; i++)
{
RightField[i] = RightSite--;
LeftField[i] = LeftSite--;//Combination계산을 위함
}
for (int k = 0; k < temp; k++)
{
for (int j = temp-1; j >= 0; j--)
{
if (RightField[k] % LeftField[j] == 0)//나누어 떨어지면 미리 나누어 놓는다. 기하급수적으로 수가 커지는걸 미리 방지하기 위함임.
{
RightField[k] /= LeftField[j];
LeftField[j] = 1;
}
}
}
for (int i = 0; i < temp; i++)
{
RightFacto *= RightField[i];//오른쪽 사이트를 Factorial계산해준다. 미리 나눠놨기 때문에 값이 크지 않다.
LeftFacto *= LeftField[i];//왼쪽 사이트를 Factorial 계산해준다.
}
cout << RightFacto/LeftFacto<<'\n';
RightFacto = LeftFacto=1;
}
return 0;
}[코드 설명 보기]
조합의 성질을 그대로 유지한 코드입니다.
가령 N이 4, M이 12가 주어졌을 때, 우리는 12C4을 구해야 합니다.

이전에 문제들을 푸셨으면 아시겠지만, 팩토리얼을 계산하는 것은 숫자의 범위를 십중팔구 넘어가 버립니다.
제가 작성한 코드에서는, 서쪽의 사이트와 동쪽의 사이트로 N과 M을 구분하고, 각각의 사이트 필드를 만들어 조합의 정의에 맞도록 1씩 감소하는 수를 넣었습니다.
int main()
{
int T, LeftSite, RightSite, temp, count = 0;
long long LeftFacto = 1, RightFacto = 1;
int LeftField[30] = { 0, }, RightField[30] = { 0, };
cin >> T;
for (int i = 0; i < T; i++)
{
cin >> LeftSite >> RightSite;//왼쪽 사이트와 오른쪽 사이트의 정보를 받는다.
temp = LeftSite;
for (int i = 0; i < temp; i++)
{
RightField[i] = RightSite--;
LeftField[i] = LeftSite--;//Combination계산을 위함
}↑입력 받고, 각각의 필드에 수를 저장합니다.
위 예시로 들었던 12C4가 이 코드에 들어간다면, 다음 사진과 같은 상태일 것입니다.

이제 하나씩 비교하며, 나눌 수 있으면 미리 나누어 놓습니다. 나중에 한 필드의 모든 값을 모두 곱해야 하므로 수가 커지기 전에 미리 처치해 놓는 것입니다.
for (int k = 0; k < temp; k++)
{
for (int j = temp-1; j >= 0; j--)
{
if (RightField[k] % LeftField[j] == 0)//나누어 떨어지면 미리 나누어 놓는다. 기하급수적으로 수가 커지는걸 미리 방지하기 위함임.
{
RightField[k] /= LeftField[j];
LeftField[j] = 1;
}
}
}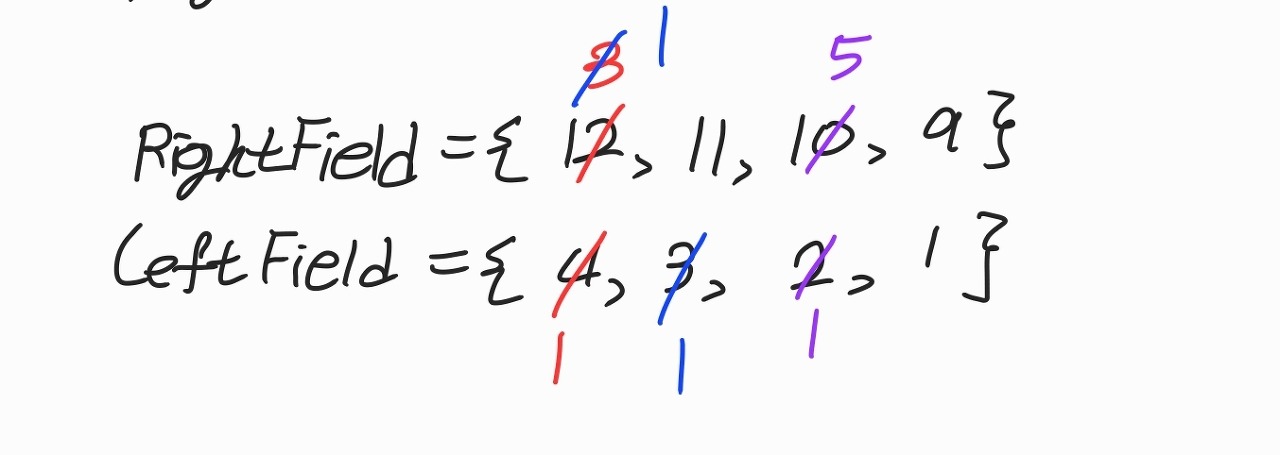
코드 실행 후 각각의 필드는 다음과 같은 상태일 것입니다.
미리 나눌 수 있는 것은 모두 나누어 놨으므로, 이제 필드 내부 모든 원소의 곱을 구하고 RightField에서 LeftField를 나누어줍니다.
for (int i = 0; i < temp; i++)
{
//오른쪽 사이트를 Factorial계산해준다. 미리 나눠놨기 때문에 값이 크지 않다.
RightFacto *= RightField[i];
//왼쪽 사이트를 Factorial 계산해준다.
LeftFacto *= LeftField[i];
}
cout << RightFacto/LeftFacto<<'\n';
RightFacto = LeftFacto=1;
}
return 0;
}'Koala - 2기 > C반' 카테고리의 다른 글
| [BOJ] 11057번. 오르막 수 (0) | 2021.01.22 |
|---|---|
| [BOJ] 14606번 피자 (0) | 2021.01.22 |
| [25411633] 2×n 타일링 - 20200118(3) (0) | 2021.01.18 |
| [13301] 타일 장식물 - 20200118(2) (0) | 2021.01.18 |
| [2748] 피보나치 수 2 - 20200118(1) (0) | 2021.01.18 |