https://www.acmicpc.net/problem/1238
1238번: 파티
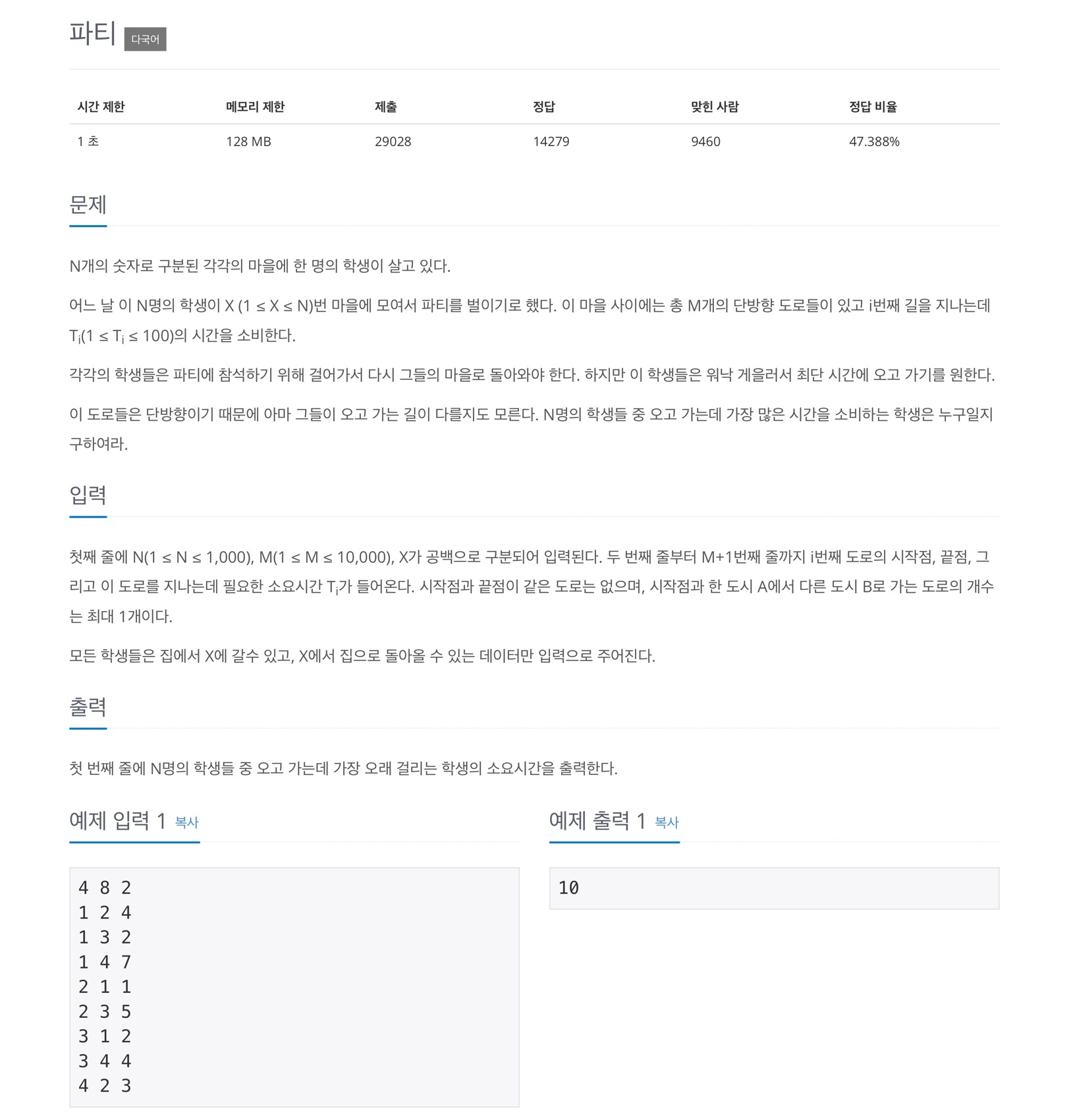
첫째 줄에 N(1 ≤ N ≤ 1,000), M(1 ≤ M ≤ 10,000), X가 공백으로 구분되어 입력된다. 두 번째 줄부터 M+1번째 줄까지 i번째 도로의 시작점, 끝점, 그리고 이 도로를 지나는데 필요한 소요시간 Ti가 들어
www.acmicpc.net
문제 설명
방향성이 있고, 간선에 가중치가 있는 그래프에서 어떤 정점이 특정한 정점 X까지 왕복하는데 가장 거리가 먼지를 찾아내는 문제입니다. 다익스트라 알고리즘으로 해결할 수 있을 것 같습니다.
문제 분석
하지만 문제가 있습니다. 왔던 정점으로 다시 되돌아가야 하는데 방향성이 있기 때문에 되돌아가는 길은 왔던 길과 다릅니다. 이 문제를 해결하기 위해서 모든 정점에서 다익스트라 알고리즘을 돌려보는 것은 너무 오래 걸립니다.
더 좋은 방법은, 방향이 반대로 된 그래프를 만들고 다익스트라 알고리즘을 돌려보는 것입니다. 원래 그래프에서 X를 root로 다익스트라 알고리즘을 돌린다면 정점 X에서 다른 모든 정점까지 가는 최단거리를 알아낼 수 있고, 방향이 반대로 된 그래프에서 다익스트라 알고리즘을 돌리면 모든 정점에서 정점 X를 도달하는 최단 거리를 알아낼 수 있습니다. 두 거리를 합치고, 최댓값을 찾으면 문제는 해결됩니다.
코드
#include<iostream>
#include<vector>
#include<queue>
#include<algorithm>
#define inf 999999999
#define pii pair<int, int>
using namespace std;
struct cmp
{
bool operator()(pii &a, pii &b)
{
return a.second>b.second;
}
};
int N, M, X;
vector<pii> graph[1001], rev_graph[1001];
vector<int> dijkstra(int start, vector<pii> graph[])
{
priority_queue<pii, vector<pii>, cmp> pq;
vector<int> dist(N+1, inf);
pii cur;
dist[start]=0;
pq.push({start, 0});
while(!pq.empty())
{
cur=pq.top();
pq.pop();
for(pii next:graph[cur.first])
{
int next_dist=dist[cur.first]+next.second;
if(next_dist<dist[next.first])
{
pq.push({next.first, next_dist});
dist[next.first]=next_dist;
}
}
}
return dist;
}
int main()
{
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
cin>>N>>M>>X;
int a, b, c;
for(int i=0; i<M; i++)
{
cin>>a>>b>>c;
graph[a].push_back({b, c});
rev_graph[b].push_back({a, c});
}
vector<int> time, rev_time, total_time;
time=dijkstra(X, graph);
rev_time=dijkstra(X, rev_graph);
for(int i=1; i<=N; i++)
{
total_time.push_back(time[i]+rev_time[i]);
}
sort(total_time.rbegin(), total_time.rend());
cout<<total_time[0];
return 0;
}'Koala - 7기 > 코딩테스트 준비 스터디' 카테고리의 다른 글
| [백준/python] 13549번 숨바꼭질 3 (0) | 2022.08.21 |
|---|---|
| [백준/Python] 1504번: 특정한 최단 경로 (0) | 2022.08.21 |
| [백준/C++] 13549번 숨바꼭질 3 (0) | 2022.08.19 |
| [백준/JAVA] 13907번 세금 (0) | 2022.08.19 |
| [백준 / Python] 7576 - 토마토 (1) | 2022.08.15 |
