https://www.acmicpc.net/problem/13549
13549번: 숨바꼭질 3
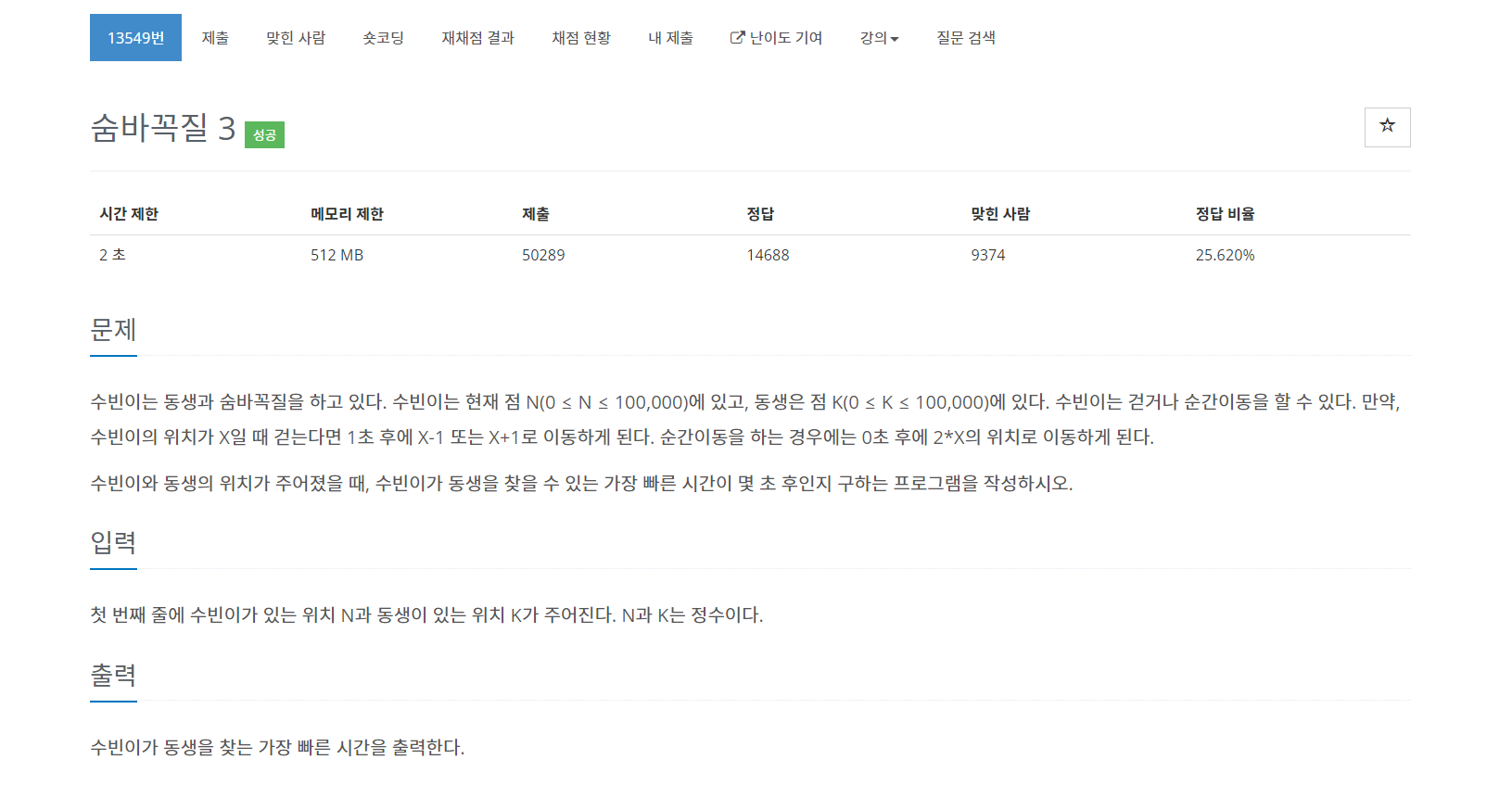
수빈이는 동생과 숨바꼭질을 하고 있다. 수빈이는 현재 점 N(0 ≤ N ≤ 100,000)에 있고, 동생은 점 K(0 ≤ K ≤ 100,000)에 있다. 수빈이는 걷거나 순간이동을 할 수 있다. 만약, 수빈이의 위치가 X일
www.acmicpc.net
문제 분석
수빈이가 동생을 찾는 가장 빠른 시간을 구하는 문제다. 수빈이는 1초에 한 칸씩 앞뒤로 걷거나, 0초에 현재 위치*2의 위치로 순간이동이 가능하다. 다익스트라 알고리즘을 사용하여 풀 수 있다.
코드
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;
#define INF 987654321
int n, k;
vector<pair<int, int>> vec[100010];
priority_queue<pair<int, int>> pq;
int dist[100010];
void dijk(int start){
dist[start] = 0;
pq.push({0, start});
while(!pq.empty()){
int cur = pq.top().second;
int cost = -pq.top().first;
pq.pop();
if(dist[cur]<cost) continue;
for(int i=0; i<vec[cur].size(); i++){
int next = vec[cur][i].second;
int ncost = vec[cur][i].first;
if(dist[next]> cost+ncost){
dist[next] = cost+ncost;
pq.push({-dist[next], next});
}
}
}
}
int main(){
cin>>n>>k;
for(int i=0; i<=100000; i++){
if(i-1>=0) vec[i].push_back({1, i-1});
if(i+1<=100000) vec[i].push_back({1, i+1});
if(i*2<=100000) vec[i].push_back({0, i*2});
}
for(int i=0; i<100010; i++){
dist[i] = INF;
}
dijk(n);
cout<<dist[k];
return 0;
}
문제 풀이
- 수빈이의 위치 n과 동생의 위치 k를 입력받는다.
- 인덱스 i 벡터에 i +-1의 위치까지 가는데 걸리는 시간 1과 i+-1, i *2의 위치까지 가는데 걸리는 시간 0과 i*2를 pair로 붂어서 push한다.
- 거리를 저장할 dist배열을 INF값을 초기화해준다.
- 수빈이는 n에서 출발하므로 n을 인자로 dijk함수를 호출한다.(다익스트라)
- dijk함수에서는 dist 출발지 값을 0으로 두고 0과 출발지를 pair로 묶어서 우선순위 큐 pq에 push한다.
- 그 후 while문을 통하여 다익스트라 알고리즘을 통해 dist배열을 채운다. cur는 현재 위치고 cost는 cur까지 가기 위해 걸리는 시간이다. 우선순위 큐는 내림차순으로 정렬되므로 시간이 적게 걸리는 것이 앞으로 오도록 -를 붙여서 cost값으로 설정한다. 그 후 for문으로 다음 위치까지 가는데 걸리는 최소 시간을 구해준다.
- dijk함수가 끝나면 dist배열에 각 위치로 가는데 걸리는 최소 시간이 저장되어 있으므로 dist[k]를 출력한다.
'Koala - 7기 > 코딩테스트 준비 스터디' 카테고리의 다른 글
| [백준/Python] 1504번: 특정한 최단 경로 (0) | 2022.08.21 |
|---|---|
| [백준/C++] 1238번 파티 (0) | 2022.08.20 |
| [백준/JAVA] 13907번 세금 (0) | 2022.08.19 |
| [백준 / Python] 7576 - 토마토 (1) | 2022.08.15 |
| [백준/Python] 4963번: 섬의 개수 (0) | 2022.08.14 |
