9465번: 스티커
첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스의 첫째 줄에는 n (1 ≤ n ≤ 100,000)이 주어진다. 다음 두 줄에는 n개의 정수가 주어지며, 각 정수는 그 위치에 해당하는 스티커의
www.acmicpc.net
동적 계획법을 통해 풀 수 있는 문제입니다.
하나의 스티커를 떼면, 맞닿아있는 3개의 스티커는 뗄 수 없게 됩니다.
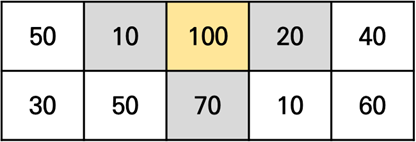
이 조건을 지키면서 각 칸마다 얻을 수 있는 최대값을 구해봅시다.
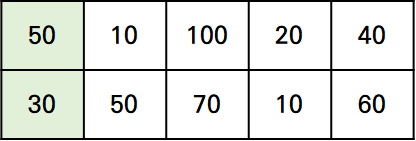
1번 열은 그대로입니다.
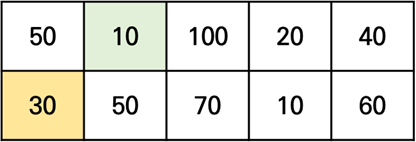

2번 열의 10점 스티커가 얻을 수 있는 최대 점수는 10+30점,
2번 열의 50점 스티커가 얻을 수 있는 최대 점수는 50+50점입니다.
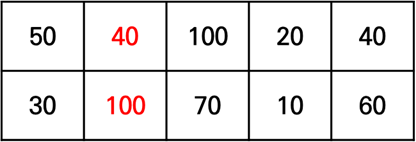
따라서 스티커를 선택했을 때 얻을 수 있는 최대 점수로 값을 바꿔줍니다.


3번 열의 100점 스티커가 선택할 수 있는 점수는 2번 열의 100점 또는 1번 열의 30점,
3번 열의 70점 스티커가 선택할 수 있는 점수는 2번 열의 40점 또는 1번 열의 50점입니다.

스티커를 선택했을 때 얻을 수 있는 최대 점수로 값을 바꿔줍니다.
위 과정을 반복해보겠습니다.
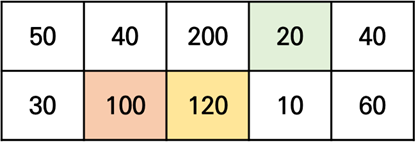
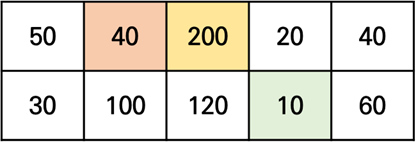


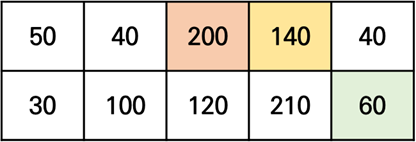

이렇게 나온 마지막 열의 두 점수 중 더 큰 값이 문제에서 요구하는 최대값이 됩니다.
점화식
점화식
if ( i = 0 )
→ score[0][i] = score[0][i]
→ score[1][i] = score[1][i]
if ( i = 1 )
→ score[0][i] = score[0][i] + score[1][i - 1]
→ score[1][i] = score[1][i] + score[0][i - 1]
if ( i >= 2 )
→ score[0][i] = score[0][i] + max( score[1][i - 1] , score[1][i - 2] )
→ score[1][i] = score[1][i] + max( score[0][i - 1] , score[0][i - 2] )
소스 코드
#include <iostream>
#include <math.h>
#include <algorithm>
#include <vector>
#include <string>
using namespace std;
// https://www.acmicpc.net/problem/9465
int T, n;
int price[2][100000];
int main()
{
cin >> T;
for (int i = 0; i < T; i++)
{
cin >> n;
for (int j = 0; j < n; j++)
{
cin >> price[0][j];
}
for (int j = 0; j < n; j++)
{
cin >> price[1][j];
}
for (int j = 1; j < n; j++)
{
if (j == 1)
{
price[0][j] += price[1][j - 1];
price[1][j] += price[0][j - 1];
}
else
{
price[0][j] += max(price[1][j - 1], price[1][j - 2]);
price[1][j] += max(price[0][j - 1], price[0][j - 2]);
}
if (j + 1 == n)
{
cout << max(price[0][j], price[1][j]) << "\n";
}
}
}
return 0;
}
'Koala - 2기 > A반' 카테고리의 다른 글
| 1932. 정수 삼각형 (0) | 2021.01.21 |
|---|---|
| [10826번]피보나치 수 4 (0) | 2021.01.19 |
| [5582번] 공통 부분 문자열 (0) | 2021.01.19 |
| 부분수열의 합 (0) | 2021.01.15 |
| [1969 번] DNA (0) | 2021.01.15 |
