https://www.acmicpc.net/problem/1010
1010번: 다리 놓기
입력의 첫 줄에는 테스트 케이스의 개수 T가 주어진다. 그 다음 줄부터 각각의 테스트케이스에 대해 강의 서쪽과 동쪽에 있는 사이트의 개수 정수 N, M (0 < N ≤ M < 30)이 주어진다.
www.acmicpc.net
1. 문제 요약
강 서쪽에는 N개의 사이트, 동쪽에는 M개의 사이트가 있다.
서쪽 사이트와 동쪽 사이트를 연결하여, 서쪽 사이트 개수만큼(N개) 다리를 지으려고 한다.
다리끼리는 서로 겹쳐질 수 없다.
이 때, 다리를 지을 수 있는 경우의 수는?
2. 문제 접근
N, M개의 사이트 간의 연결을 "더 적은 개수의 사이트 간의 연결"들의 합으로 표현할 수 있다고 판단하여, DP를 사용하기로 하였습니다. DP(다이나믹 프로그래밍 혹은 동적 계획법)는 하나의 큰 문제를 여러 개의 작은 문제로 나누고, 작은 문제들의 결과를 저장하여 다시 큰 문제를 해결할 때 사용하는 문제해결 패러다임입니다.
점화식을 만들기 전, 문제의 변수부터 파악합니다. N-M개 사이트 간 N개의 다리를 지을 수 있는 경우의 수를 구하는 문제이므로, 변수는 N과 M이 됩니다.
이제 점화식을 만들어봅니다. 문제에 주어진 조건을 활용하여 점화식에 필요한 규칙들을 뽑아냅니다.
- N이 1일 때, 경우의 수는 M개이다 : 다리가 1개이므로 겹치는 경우가 발생하지 않아 다리를 짓는 case가 M개 존재합니다.
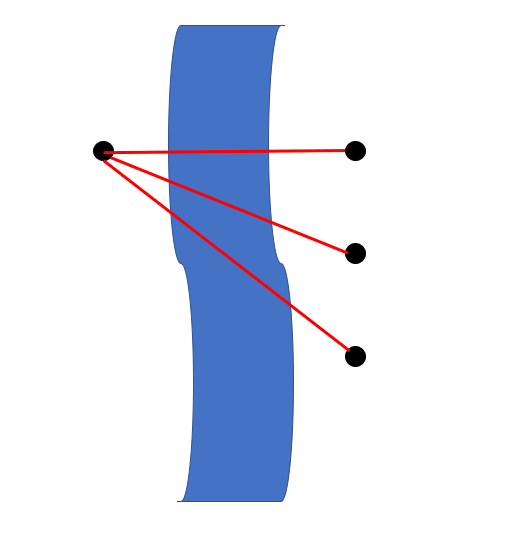
- N이 2 이상일 때, 기준선을 기준으로 나머지 사이트들을 연결하는 경우의 수 구하여(작은 문제) 합하기(큰 문제 해결)
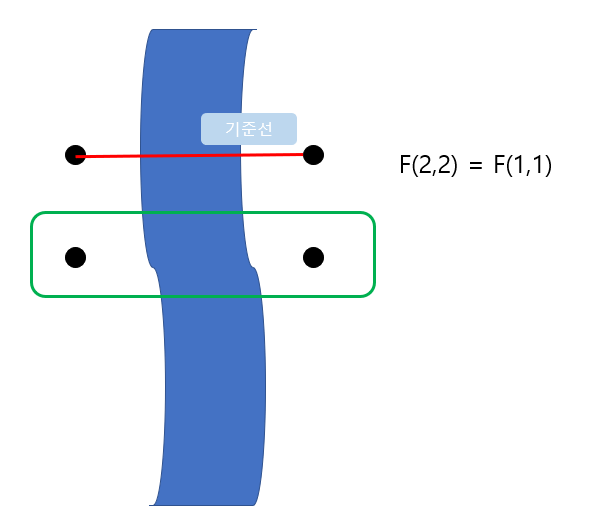
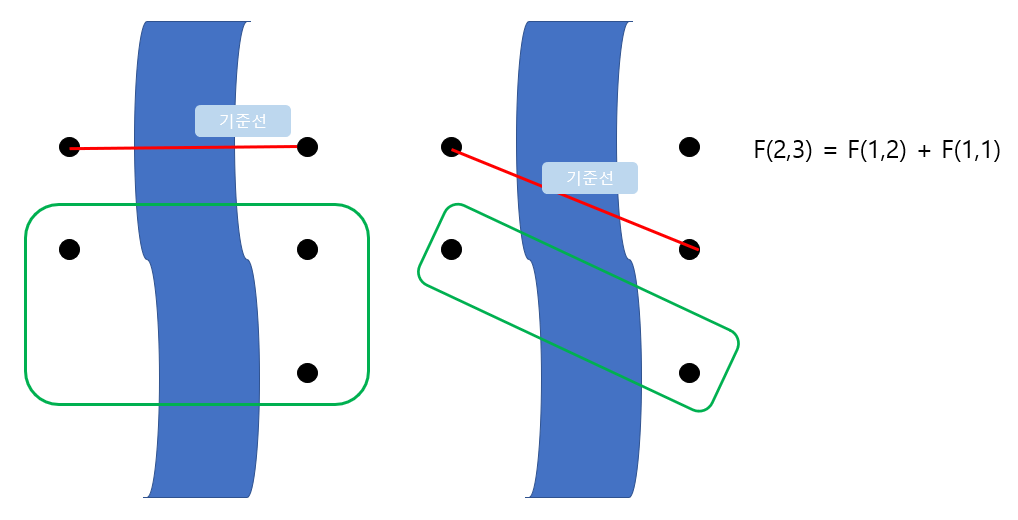
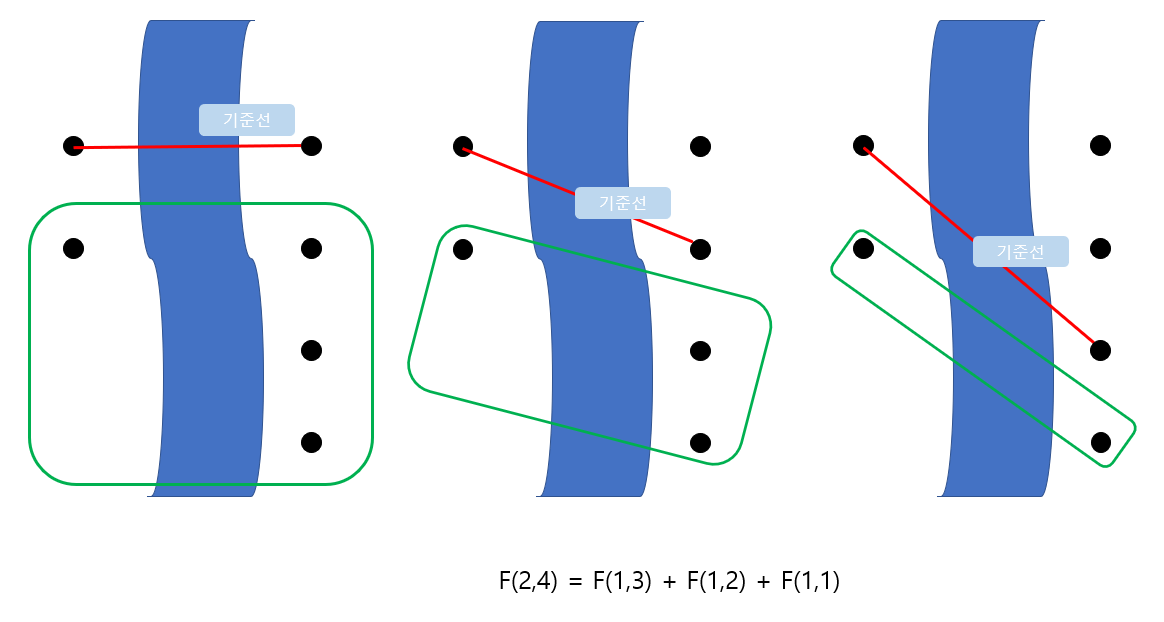
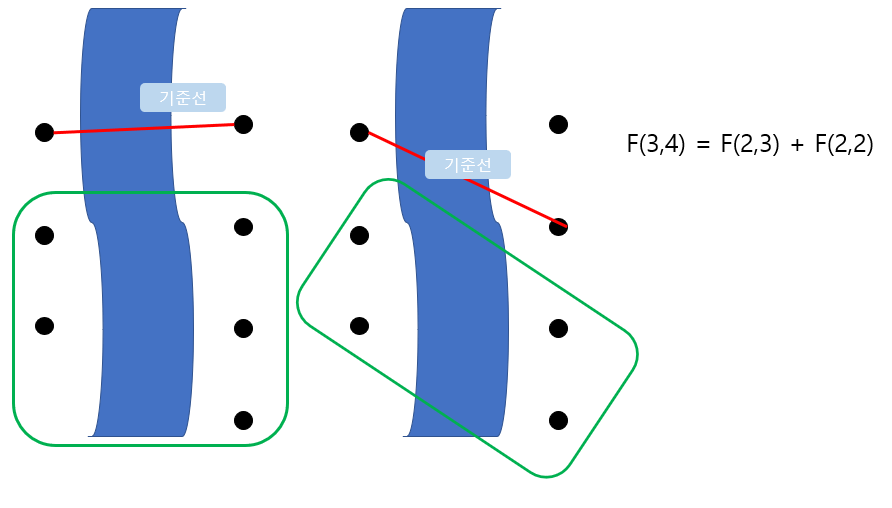
위와 같은 규칙을 통해 만든 점화식은 아래와 같습니다.
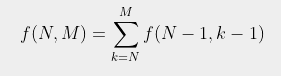
3. 구현하기
Bottom-Up 방식으로 DP를 구현합니다. Bottom-Up 방식이란 아래에서부터 계산을 수행하고 그 값을 누적시켜서 전체 큰 문제를 해결하는 방식입니다.
- dp라는 2차원 배열을 만들고
- 이미 알고 있는 값인 N=1일 때의 상태를 우선 저장해주고( dp[1][i] )
- 해당 값들을 합해나가며 dp 배열을 채워나가고
- 최종적으로 목표값인 dp[N][M]를 구해주겠습니다.
import sys
input = sys.stdin.readline
def bridge(n, m):
dp = [[0 for _ in range(m+1)] for _ in range(n+1)]
for i in range(1, m+1): dp[1][i] = i # N = 1일 때
# N이 2 이상일 때
for i in range(2, n+1):
for j in range(i, m+1):
for k in range(j, i-1, -1):
dp[i][j] += dp[i-1][k-1]
return dp[n][m]
T = int(input())
for _ in range(T):
N, M = map(int, input().split())
print(bridge(N,M))
4. 느낀점
DP는 이 문제가 DP인지 깨닫고, 어떻게 작은 단위의 문제로 쪼갤지 고민하고, 점화식을 만들고, 실제로 구현하는 것까지 A to Z 모두 어려운 것 같습니다. 꾸준하게 다양한 문제를 풀어보며 DP 문제에 대한 감을 높여가는 것이 중요하리라 생각됩니다.
'Koala - 9기 > 코딩테스트 준비 스터디' 카테고리의 다른 글
| [백준/Java] 2293번 동전1 (0) | 2023.01.11 |
|---|---|
| [백준/C++] 2565번 전깃줄 (0) | 2023.01.11 |
| [백준/C++] 2631번 줄세우기 (LCS) (0) | 2023.01.10 |
| [백준/Python] 25497번: 기술 연계마스터 임스 (0) | 2023.01.08 |
| [백준/node.js] 18429번 근손실 (0) | 2023.01.08 |