https://www.acmicpc.net/problem/1018
1018번: 체스판 다시 칠하기
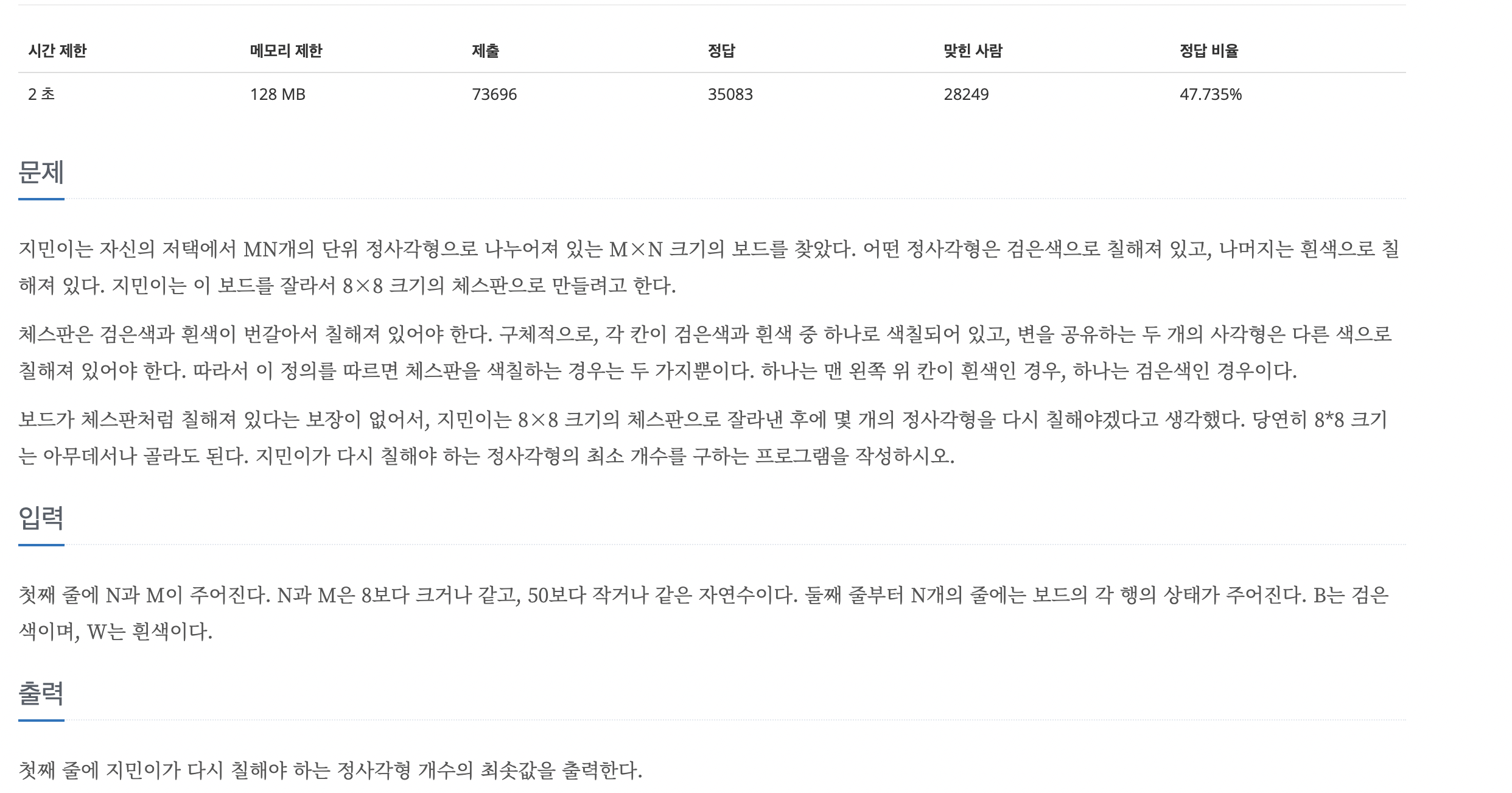
첫째 줄에 N과 M이 주어진다. N과 M은 8보다 크거나 같고, 50보다 작거나 같은 자연수이다. 둘째 줄부터 N개의 줄에는 보드의 각 행의 상태가 주어진다. B는 검은색이며, W는 흰색이다.
www.acmicpc.net
문제
문제 분석
나는 이 문제를 정상적인 체스판과 '다른' 부분들의 개수를 찾는 것이라고 생각했다. 여기서 정상적인 체스판이란 8 x 8의 W부터 시작하는 체스판과 B부터 시작하는 체스판, 2 종류이다. 프로그래밍이니 B와 W라는 표현은 적합하지 않으므로, 각각 0과 1로 치환하여 2차원 벡터를 만들었다. => 이 두 벡터는 chess1, chess2라 명명한다.
멀쩡한 체스판과 '다른' 타일의 개수를 찾는다는 것은, 내적을 의미한다. 물론 통상적인 내적연산인 a1 * b1 + a2 * b2 + ...가 아닌, '다른' 것을 찾는 것이기에 XOR연산을 통해 내적연산을 변형한다. 즉, 내가 사용할 내적 연산은 a1^b1 + a2^b2 + ...가 되겠다.
입력받는 보드의 크기는 8 x 8 보다 크거나 같을 것이므로 해당 내적연산을 체스판을 1칸씩 상하좌우로 움직여가며 행하며, 이 모든 '다른'타일들의 개수, 즉 내적연산의 결과값들을 모두 따로 벡터에 저장하여 그 중 최솟값을 찾는다.
정상적인 체스판의 종류는 앞서 말했듯 두 종류이므로 내적 연산도 두번씩 한다.
코드
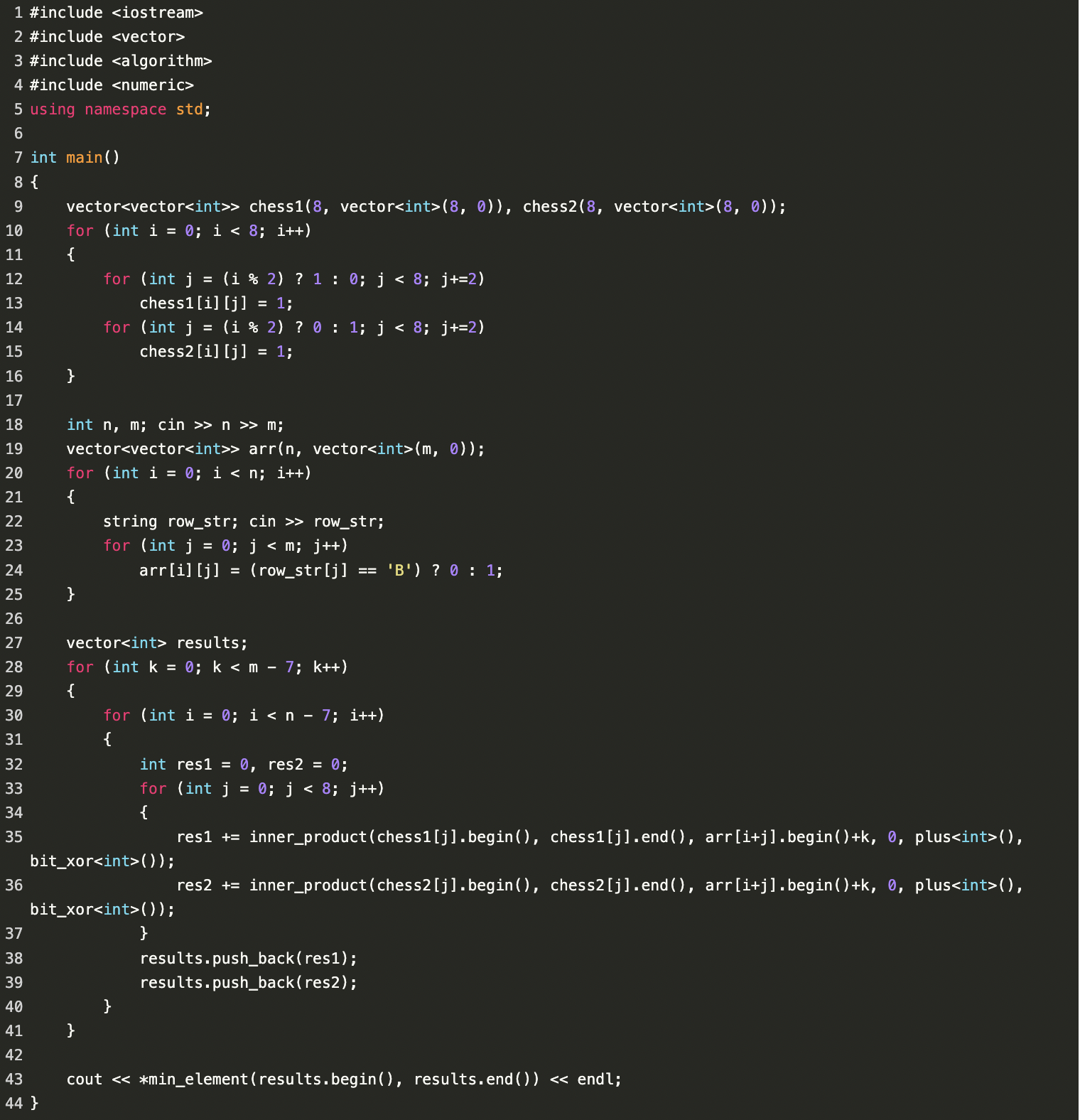
초반에 체스판들을 이리저리 옮겨가며 내적값들을 구하는 for문 안에서 index값들이 머릿속에서 꼬여 엄청 헷갈렸었다. 덕분에 이번 주차 문제들 중 푸는 법을 일찍이 알았음에도 구현이 어려워 가장 오래걸렸던 문제였기에 기억에 남는다.
'Koala - 7기 > 기초 알고리즘 스터디' 카테고리의 다른 글
| [백준/python] 2999번 비밀 이메일 (1) | 2022.08.07 |
|---|---|
| [백준/Python] 11179 2진수 뒤집기 (1) | 2022.08.07 |
| [백준/Python] 2729 이진수 덧셈 (1) | 2022.08.07 |
| [백준/Python] 14915번 회문 (2) | 2022.08.03 |
| [백준/python] 10773번 제로 (1) | 2022.08.01 |
