푸시느라 고생하셨습니다~

문제 구성
- 백준 8911번 거북이
- 백준 15500번 이상한 하노이 탑
- 백준 1461번 도서관
이번 문제는 간단한 시뮬레이션 문제, 조금 생각하면 구현은 간단한 스택 문제,
난이도 있는 정렬 + 그리디 문제를 가져왔습니다!
시뮬레이션 문제와 마지막 문제의 난이도를 고려해 3문제만 넣어두었지만, 핵심만 빠르게 파악한다면 금방 푸실 거라 생각됩니다. (앗! 벌써 18분 만에 다 푸신분이 나오셨네요 ㅠㅠ)
1. 백준 8911번 거북이
문제에서 하라는 대로 하면되는, 시뮬레이션 문제입니다.
핵심은 방향 전환과, 경로에 따라 정답이 되는 가장 작은 직사각형의 넓이를 어떻게 구하느냐겠네요.
우선 방향 전환 설명에 앞서, 기본적으로 4방향 (동, 서, 남, 북)으로 이동하는 격자판이 주어졌을 때 가장 먼저 할 일은 각 방향에 따른 움직임을 배열로 저장하는 것이 좋습니다.
예시 코드
// 동, 서, 남, 북
int dy[] = { 0, 0, 1, -1 };
int dx[] = { 1, -1, 0, 0 };
이렇게 저장하게 되면, 만약 동쪽으로 이동한다! 싶으면 기존 좌표 (y, x)에서 (y + 0, x + 1) 만큼 이동하는 거예요!
그럼 방향 전환도 간단히 배열 처리를 할 수 있습니다.
예시 코드
//각 방향마다 {좌회전, 우회전}
pair<int, int>rot[4] = { {3, 2}, {2, 3}, {0, 1}, {1, 0} };저는 정수 0 ~ 3 까지를 순서대로 동, 서, 남, 북으로 지정했기 때문에
배열의 인덱스를 방향 값으로 생각한다면, 첫 번째 원소를 좌회전 시 바뀌는 방향으로, 두 번째는 우회전 시 바뀌는 방향으로 생각해 저장해두었습니다.
예를 들어 방향값 0인 동쪽을 바라보고 있었다면, 좌회전하면 3으로 북쪽이 되고, 우회전하면 2로 남쪽을 바라보게 됩니다.
이런 부분은 사소하지만, 시뮬레이션 문제에서 나보다 훨씬 빠르게 푸는 사람들이 있다면 사전에 이런 처리를 해두었을 가능성이 높으니 익숙해지셔야 합니다!
이렇게 방향에 대한 기본적인 세팅이 다 되었다면, 이제 가장 작은 직사각형을 구해봅시다!
가장 작은 직사각형은 간단하게 경로를 이동할 때 지나치는 모든 거북이의 좌표를 보면서
x좌표가 최대, 최솟값, y좌표의 최대, 최솟값을 바꾸어주면 됩니다.
만약 시작 지점 (0, 0)에서 방향 회전 없이 전진을 했다면, 거북이는 북쪽 (y = y - 1)로 이동했기 때문에
y좌표의 최솟값은 -1로 변하겠죠.
이렇게 모든 최대, 최솟값을 구했다면 정답은 (x최대 - x최소) x (y최대 - y최소)가 됩니다.
소스 코드(.cpp)
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
//각 idx 당 {좌회전, 우회전}
pair<int, int>rot[4] = { {3, 2}, {2, 3}, {0, 1}, {1, 0} };
//전진, 후진
int dy[] = { 0, 0, 1, -1 };
int dx[] = { 1, -1, 0, 0 };
int main() {
ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
int t; cin >> t;
while (t--) {
string s; cin >> s;
int dir = 3;
int y = 0, x = 0;
int max_x = 0, min_x = 0, max_y = 0, min_y = 0;
for (int i = 0; i < s.size(); i++) {
if (s[i] == 'F') {
y += dy[dir];
x += dx[dir];
max_x = max(max_x, x); min_x = min(min_x, x);
max_y = max(max_y, y); min_y = min(min_y, y);
}
else if (s[i] == 'B') {
y -= dy[dir];
x -= dx[dir];
max_x = max(max_x, x); min_x = min(min_x, x);
max_y = max(max_y, y); min_y = min(min_y, y);
}
else if (s[i] == 'L') {
dir = rot[dir].first;
}
else {
dir = rot[dir].second;
}
}
int ans = (max_y - min_y) * (max_x - min_x);
cout << ans << "\n";
}
return 0;
}
2. 백준 15500번 이상한 하노이 탑
스택 문제이긴 하나, 스택의 개념만 알 수 있다면 풀 수는? 있는 문제입니다.
이 문제에서 고려해야 할 점은 크게 두 가지입니다.
우선 원판을 옮긴 횟수가 12345 보다 같거나 작도록 구현하는 부분은 문제의 기본 조건이기 때문에 중요합니다.
두 번째는 출력을 어떻게 할 것인지 생각해야 합니다.
첫 번째 옮긴 횟수가 12345보다 작게 구현하는 방법은 조건을 만족하는 모든 n에 대해서 (n <= 123)
간단히 증명 가능합니다.
우선 최악의 경우, 우리의 목표인 3번 장대에 놓아야 할 원판이 계속 맨 아래 있다고 가정해봅시다.
이 경우 입력 값은 n, n-2,..., n-3, n-1 이런 식으로 주어지겠죠. 찾으려는 수가 n일 때 n-1개의 원판을 다 빼내야 n이 나온다는 의미입니다.
만약 n이 범위에서 가장 큰 123이라면, 우리는 원판을 빼내는 과정을 123, 122, 121,..., 1번 해내야 합니다.
따라서 최악의 경우 원판을 옮긴 횟수 k는 (123 * 124) / 2 = 7,626번이 되므로 무슨 입력 값이 주어지더라도 원판을 옮길 수 있음이 증명되었습니다.
또한 이 과정, 구현하려고 생각해보면 딱히 어렵지 않습니다!
장대는 1, 2, 3 총 3개인데, 그냥 3번 장대로 옮기고 싶은 숫자 나올 때까지
1번 장대에 있는 원판들을 차례대로 2번으로 옮기다가, 찾고 있는 숫자가 나오면 3번으로 빼고, 다시 2번으로 옮기고
이제 반대로
2번 장대 원판들을 1번으로 옮기고.. 과정을 반복하면 됩니다.
만약 원하는 원소가 연속으로 나오면 어떡하냐고요? 그럼 더 좋죠! 찾는 숫자 나올 때마다 3번으로 빼고, 찾는 숫자 -= 1로 바꿔주면서 또 찾으면 3번으로 빼주면 됩니다.
이 장대의 특성은 먼저 들어가면 나중에 나오므로 스택을 통해 구현해주면 됩니다.
이제 출력을 해야 할 차례입니다.
옮기는 횟수 k는 단 번에 알 수 없으므로, 원판을 옮길 때마다 (스택의 pop, push 과정) 어디에서 어디로 가는지 벡터에 저장해 두고, 벡터의 크기를 출력해주면 됩니다.
소스 코드(.cpp)
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int main() {
ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
int n; cin >> n;
stack<int>st1, st2;
for (int i = 0; i < n; i++) {
int tmp; cin >> tmp;
st1.push(tmp);
}
vector<pair<int, int> >ans;
int idx = n; //3번 장대로 옮겨야할 원판 idx
bool flag = true; //true : st1, false : st2 차례
while (idx > 0) {
if (flag) {
while (!st1.empty()) {
if (st1.top() == idx) {
ans.push_back({ 1, 3 });
st1.pop();
idx--;
}
else {
ans.push_back({ 1, 2 });
st2.push(st1.top());
st1.pop();
}
}
flag = false;
}
else {
while (!st2.empty()) {
if (st2.top() == idx) {
ans.push_back({ 2, 3 });
st2.pop();
idx--;
}
else {
ans.push_back({ 2, 1 });
st1.push(st2.top());
st2.pop();
}
}
flag = true;
}
}
cout << ans.size() << "\n";
for (int i = 0; i < ans.size(); i++) cout << ans[i].first << " " << ans[i].second << "\n";
return 0;
}
3. 백준 1461번 도서관
기본적인 정렬에 그리디적 생각을 추가해야 하는.. 딱 골드 5 문제입니다.
우선 저는 문제를 이런 식으로 정리해두었습니다.
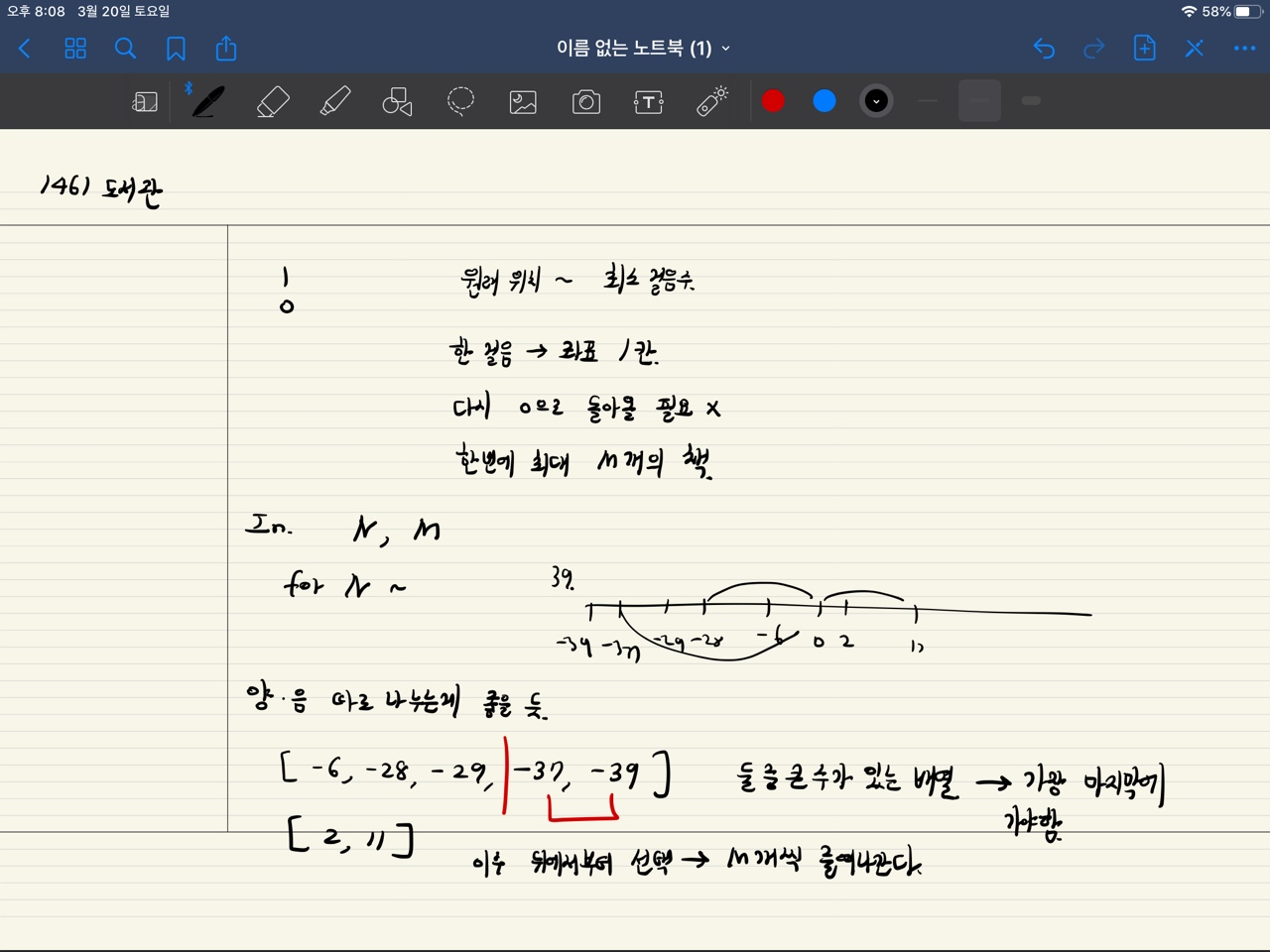
글씨가 좀 못나긴 하지만..
보통 문제 정리를 하고, 입력, 출력 값을 기록해둔 후에
테스트 케이스에 따라 어떤 과정을 거치는지 생각해봅니다.
여기서 기록해둔 대로라면, 우선 문제에서 좌표는 양수, 음수 둘 다 나올 수 있는데
0이 책을 가지고 가는 기준점이기 때문에 양수와 음수는 나누어 고려해야 합니다.
만약 3개의 책을 한 번에 가지고 갈 수 있는데 (-2, 1, 2) 좌표로 가져간다면 딱히 좋은 방향은 아니죠.
그냥 (-2), (1,2)로 나눠 가는 것이랑 똑같은 행동입니다.
그리고 문제에서 중요한 "다시 0으로 돌아올 필요가 없다"라는 부분도 중요합니다.
다시 0으로 돌아올 필요가 없다는 것은 책 배송이 다 끝났음을 의미합니다. 따라서 마지막에만 다시 0으로 갈 필요가 없죠.
즉, 왕복이 아닌 편도로 보낼 수 있다는 건데, 이 과정은 좌표가 가장 큰 놈에게 주는 게 가장 유리합니다.
그냥 발로 생각해도 그렇습니다.
그럼 여기까지 생각을 했고, 첫 번째 테스트 케이스를 생각해보면
(2, 11) 구간 왕복 +22
(-29, -28) 구간 왕복 +58
(-6) 구간 왕복 +12
(-39, -37) 구간 편도 +39
총 +131의 비용이 들었습니다.
처음에는 (-6, -28) 이런 식으로 낮은 수부터 묶었으나, 테스트 케이스를 생각해보니 큰 수부터 묶는 것이 좋다는 판단을 하게 되었네요.
따라서 문제는 양수, 음수 정렬을 각각 한 후에 큰 수부터 (음수들은 양수로 바꿔주는 것이 좋습니다!)
m개씩 묶어 처리를 하되,
양수, 음수 합쳐서 절댓값이 가장 높은 수는 따로 먼저 처리를 해주는 게 좋습니다. (편도로 계산)
소스 코드(.cpp)
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int main() {
ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
int n, m;
cin >> n >> m;
vector<int>v(n);
for (int i = 0; i < n; i++) cin >> v[i];
vector<int>plus, minus;
//음수, 양수 나누기
for (int i = 0; i < n; i++) {
if (v[i] > 0) plus.push_back(v[i]);
else minus.push_back(-v[i]);
}
//정렬
sort(plus.begin(), plus.end());
sort(minus.begin(), minus.end());
//각각, 마지막 부분의 인덱스값 저장
int plus_ptr = plus.size() - 1;
int minus_ptr = minus.size() - 1;
int ans = 0;
//둘 중 하나가 비어있다면, 마지막에 어느쪽이 돌아오지 않을 것인지 고려할 필요 없다.
if (plus.empty() || minus.empty()) {
if (plus.empty()) {
while (minus_ptr >= 0) {
//맨 끝 부분은 돌아오지 않는다.
if (minus_ptr == minus.size() - 1) {
ans += minus[minus_ptr];
minus_ptr -= m;
}
//나머지는 2배
else {
ans += 2 * minus[minus_ptr];
minus_ptr -= m;
}
}
}
else {
while (plus_ptr >= 0) {
if (plus_ptr == plus.size() - 1) {
ans += plus[plus_ptr];
plus_ptr -= m;
}
else {
ans += 2 * plus[plus_ptr];
plus_ptr -= m;
}
}
}
}
else {
//둘 중 더 큰 수를 가지고 있는 쪽을 마지막에 돌아오지 않게 한다.
if (plus.back() > minus.back()) {
while (plus_ptr >= 0) {
if (plus_ptr == plus.size() - 1) {
ans += plus[plus_ptr];
plus_ptr -= m;
}
else {
ans += 2 * plus[plus_ptr];
plus_ptr -= m;
}
}
while (minus_ptr >= 0) {
ans += 2 * minus[minus_ptr];
minus_ptr -= m;
}
}
else {
while (minus_ptr >= 0) {
if (minus_ptr == minus.size() - 1) {
ans += minus[minus_ptr];
minus_ptr -= m;
}
else {
ans += 2 * minus[minus_ptr];
minus_ptr -= m;
}
}
while (plus_ptr >= 0) {
ans += 2 * plus[plus_ptr];
plus_ptr -= m;
}
}
}
cout << ans << "\n";
}'Koala - 3기' 카테고리의 다른 글
| 4/24 모의 테스트 해설 (0) | 2021.04.25 |
|---|---|
| 4/3 모의 테스트 해설 (0) | 2021.04.03 |
