

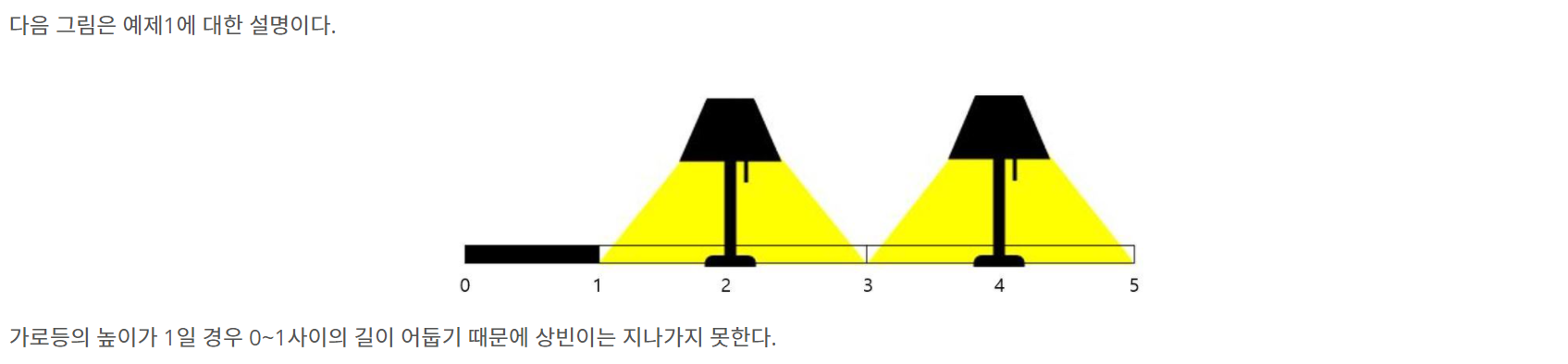

풀이 1
가로등의 위치는 정해져있고 0부터 N까지의 돌다리를 밝혀야 한다.
가로등은 가로등의 위치(pos)에서 가로등의 높이(h)만큼 양 옆으로 밝힐 수 있다.
높이가 높아질수록 비용이 많이 든다 최소 비용을 위해 가로등 높이는 최소가 되어야한다.
1. 가로등의 높이를 x라고 가정하고 생각했을 때 h가 x인 상황에서 돌다리를 전부 밝힐 수 있는지 없는지를 판별할 수 있다.
2. 가로등의 높이가 x일때 돌다리가 전부 밝혀진다면 x보다 높은 높이는 당연히 모든 돌다리를 밝힐 수 있다.
위의 두가지 조건에 의해서 Parametric Search를 이용할 수 있다.
가로등 높이가 될 수 있는 범위(left~right)내에서 이분탐색의 아이디어를 이용하여 특정 높이를 정하고(mid = (left+right)/2) 해당 높이로 돌다리를 전부 밝힐 수 있는지 판별한다. 만약 밝힐 수 있다면 가로등의 최소 높이를 구하는 것이기 때문에 mid보다 더 작은 값(right = mid -1)을 시도해본다. 밝힐 수 없다면, mid보다 더 높은 값(left = mid + 1)을 시도한다. 위의 순서를 반복하면 더 이상 시도해 볼 수 없는 상황(left > right)이 발생하므로 프로그램은 종료하게 된다.
가로등의 높이에 따라 돌다리를 전부 밝힐 수 있는지를 판별하기 위해 가장 앞의 가로등 부터 불을 켜본다고 생각한다면 이해하기 쉽다. 맨 앞의 처음에는 0부터 N까지의 돌다리가 모두 깜깜하다 즉 깜깜한 부분의 시작점(darkStart)은 0이다. 맨 앞의 가로등을 켜서 이 왼쪽 가로등 불빛(pos - h)이 어두운 부분의 시작점보다 작다면 오른쪽 가로등 불빛에서부터 다시 어두운 부분이 시작된다. 만약 크다면 전체 돌다리를 밝힐 수 없다. 위를 반복하여 깜깜한 부분이 사라진다면 전체를 밝힌다는 의미가 된다.
소스코드1
#include <iostream>
#include <vector>
using namespace std;
bool isPossible(vector<int>& pos, int n, int h);
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int n, m;
cin >> n >> m;
vector<int> pos(m);
for(int i = 0; i < m; ++i) {
cin >> pos[i];
}
int left = 1, right = n;
int mid, ans = 0;
while(left <= right) {
mid = (left+right)/2;
if(isPossible(pos, n, mid)) {
ans = mid;
right = mid - 1;
} else {
left = mid + 1;
}
}
cout << ans << "\n";
return 0;
}
bool isPossible(vector<int>& pos, int n, int h) {
int len = pos.size();
int darkStart = 0;
for(int i = 0; i < len; ++i) {
if(pos[i]-h <= darkStart) {
darkStart = pos[i] + h;
} else break;
}
return n - darkStart <= 0;
}'Koala - 2기 > C반' 카테고리의 다른 글
| [BOJ] 2346번. 풍선 터뜨리기 (0) | 2021.02.18 |
|---|---|
| [1072번] 게임 (0) | 2021.02.03 |
| Unordered_set : 호다닥 찾아버리기(+BOJ 수찾기) (0) | 2021.02.02 |
| 9517번 i love croatia (0) | 2021.01.25 |
| 2949번 나무조각 (0) | 2021.01.25 |
